Hilbert's Third Problem
Introduction
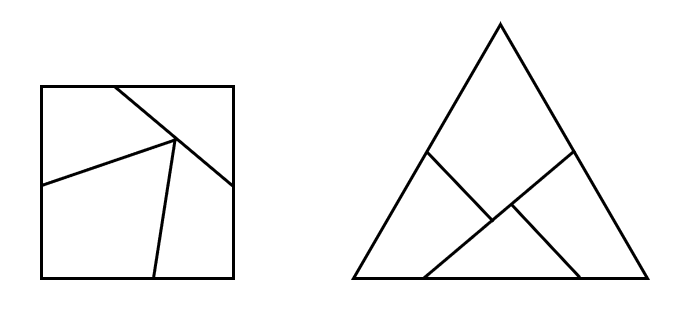
정사각형을 정삼각형으로 만들 수 있을까요? 다시말해, 정사각형을 유한개의 조각으로 분할해 넓이가 같은 정삼각형으로 만들 수 있을까요? 답은 가능하다입니다. 아래와 같이 분할하여 만들 수 있으며, 실제로 조각이 가장 적은 구성임이 최근 증명되었습니다.
심지어 임의의 넓이가 같은 두 다각형 $P$, $Q$에 대해서 $P$를 유한 개의 조각으로 잘라 $Q$를 구성할 수 있음이 증명되었습니다. (Wallace-Bolyai-Gerwien theorem)
증명은 간단하게 다음과 같이 할 수 있습니다.
- 임의의 다각형은 삼각분할이 가능하다.
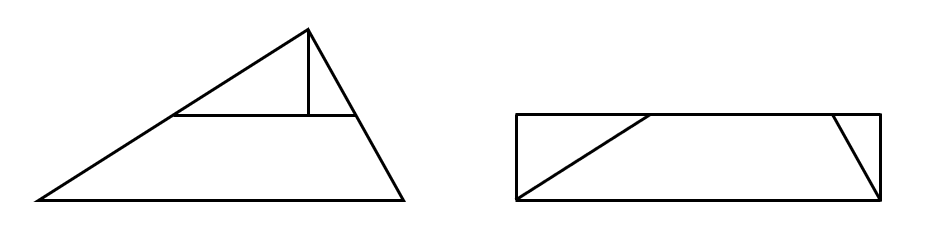
- 임의의 삼각형을 직사각형으로 만들 수 있다.
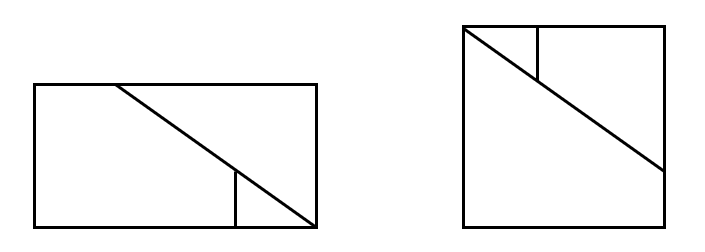
- 임의의 직사각형을 정사각형으로 만들 수 있다.
- 두 정사각형을 큰 하나의 정사각형으로 만들 수 있다.
- 1~4에서, 임의의 다각형은 삼각분할을 하여 각각을 직사각형으로 만든 뒤, 정사각형을 만들어 큰 정사각형으로 만들 수 있다.
- 따라서 $P$를 정사각형으로 만든 뒤 이를 $Q$에서 정사각형을 구성하는 과정을 역으로 시행하면 $Q$를 구성할 수 있다.
이때 2, 3, 4는 다음과 같은 그림으로 바로 얻을 수 있습니다.
그렇다면, 위 문제를 3차원으로 확장시킨다면 어떻게 될까요? 이 문제가 바로 힐베르트의 3번 문제입니다. 즉, 다음과 같이 기술할 수 있습니다:
- 임의의 부피가 같은 두 다면체 $P$, $Q$에 대해, $P$를 유한 개의 조각으로 잘 잘라 붙여 $Q$를 만들 수 있는가?
위 문제는 Dehn이 Dehn invariant라는 개념을 도입하여 부정적으로 해결하였고, 추후 V.F.Kagan 등이 단순화된 풀이를 제시하였습니다.
Equidecomposable / Equicomplement
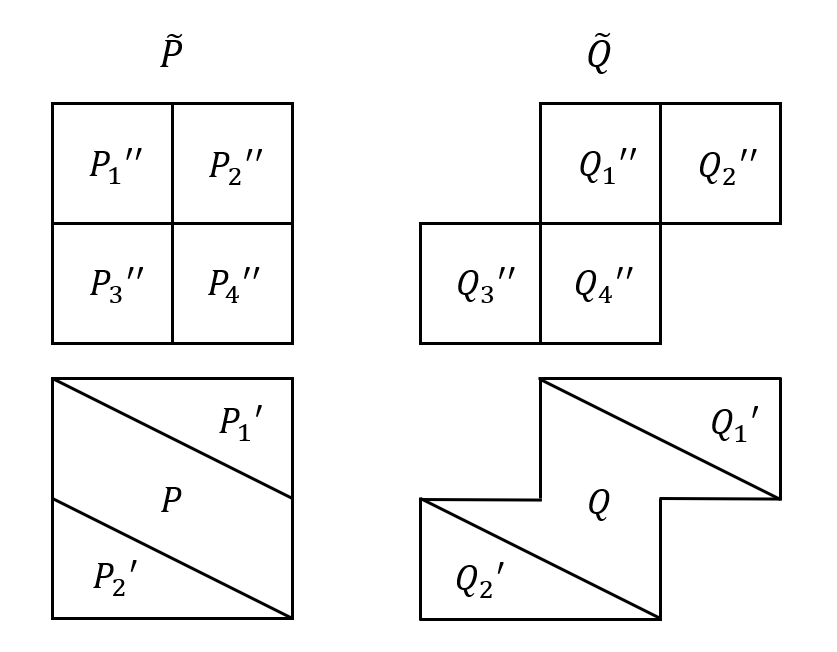
두 다면체 $P$, $Q$에 대해, 이를 각각 $P_i$와 $Q_i$가 합동이도록 $P_1, \cdots, P_n$과 $Q_1, \cdots, Q_n$으로 분할 가능하다면, $P$와 $Q$가 equidecomposable하다고 합니다.
그리고, 두 다면체 $P$, $Q$에 대해, 어떤 equidecomposable한 다면체 $\tilde{P} = P_1’’ \cup \cdots \cup P_n’‘$와 $\tilde{Q} = Q_1’’ \cup \cdots \cup Q_n’‘$가 존재하여 어떤 합동인 $P_i’, Q_i’$들에 대해 $\tilde{P} = P \cup P_1’ \cup P_2’ \cup \cdots \cup P_m’$과 $\tilde{Q} = Q \cup Q_1’ \cup Q_2’ \cup \cdots \cup Q_m’$를 만족시키면 $P$와 $Q$가 equicomplete하다고 합니다.
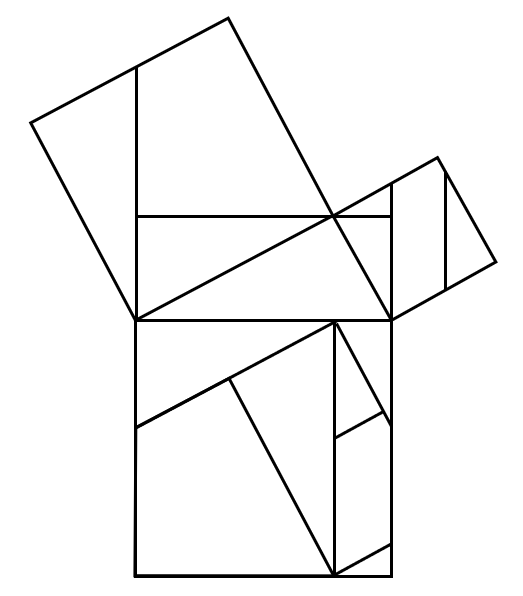
이해를 돕기 위해 아래와 같은 그림을 가져와보면, 그림에서 $\tilde{P}$와 $\tilde{Q}$는 equidecomposable하고, $P$와 $Q$는 equicomplete합니다.
이제 두 다면체가 equidecomposable 혹은 equicomplement한지를 판단하기 위해 필요한 두 가지 보조정리에 대해 살펴봅시다.
The Cone Lemma
(Lemma) 정수계수 선형연립방정식이 양의 실수해를 갖는다면, 양의 정수해도 갖는다.
증명은 다음과 같습니다.
먼저 위를 수학적으로 기술하면, 각 원소가 정수인 행렬 $A \in \mathbb{Z}^{M \times N}$에 대해 \(C = \{ \mathrm{x} \in \mathbb{R}^N : A\mathrm{x} = \mathrm{0}, \mathrm{x} > \mathrm{0} \}\) 가 공집합이 아니면, 정수인 점 또한 가짐을 보이면 됩니다.
$C$가 공집합이 아니면, $\mathrm{x}$에 적절히 상수배를 취해 모든 coordinate들을 $1$ 이상으로 만들어 줄 수 있으므로 $\overline{C} = { \mathrm{x} \in \mathbb{R}^N : A\mathrm{x} = \mathrm{0}, \mathrm{x} \geq \mathrm{1} }$도 공집합이 아님을 알 수 있습니다.
만약 $\overline{C} \subseteq C$가 유리수 점을 가짐을 보인다면, 모든 coordinate에 분모의 최소공배수를 곱해 주어 정수 점을 얻을 수 있으므로, $\overline{C}$가 유리수 점을 가진다는 것을 보이면 충분합니다.
이제 이를 증명하기 위한 많은 방법 중 “Fourier-Motzkin elimination”을 소개하겠습니다.
각 원소가 정수인 행렬 $A$에 대해 $A\mathrm{x} = \mathrm{0}, \mathrm{x} \geq \mathrm{1}$은 사전적으로(Lexicographically) 가장 작은 유리수해를 가짐을 증명할 것입니다. 이때 각 column vector $\mathrm{a}$에 대해 $\mathrm{a}^T \mathrm{x} = 0$은 $\mathrm{a}^T \mathrm{x} \geq 0$과 $-\mathrm{a}^T \mathrm{x} \geq 0$로 나타낼 수 있고, 따라서 각 원소가 정수인 행렬 $A$와 $\mathrm{b}$에 대해
\[A\mathrm{x} \geq \mathrm{b}, \mathrm{x} \geq \mathrm{1}\]을 만족시키는 실수해가 존재할 때, 사전적으로 가장 작은 해의 모든 coordinate가 유리수임을 보이면 충분합니다.
이를 $N$에 대한 귀납법으로 보여봅시다. 먼저 $N=1$일 때는 자명합니다. 이제 $N>1$일 때를 살펴보면, 만약 $\mathrm{x}’ = (x_1, \cdots, x_{N-1})$가 고정되어 있다고 할 때 부등식들을 $x_N$에 대해 풀면 $x_N$에 대한 lower bound($x_N \geq 1$ 포함) 또는 upper bound들을 얻을 수 있습니다. 이때 임의의 lower bound가 임의의 upper bound 이하라는 것으로부터 $x_1, \cdots, x_{N-1}$들에 대한 부등식을
\[A' \mathrm{x}' \geq \mathrm{b}, \mathrm{x}' \geq \mathrm{1}\]와 같이 얻을 수 있습니다. 귀납법에 의해 이는 사전적으로 가장 작은 해 $x’_*$를 얻으며, 이는 유리수해입니다. 이를 이용해 선형 방정식 혹은 부등식을 풀어 가장 작은 $x_N$을 얻을 수 있고, 이때 방정식 또는 부등식의 계수가 모두 정수이므로 유리수임을 알 수 있습니다. 그리고 이는 사전적으로 가장 작은 해이고, 따라서 귀납적으로 위 정리가 증명됩니다.
The Pearl Lemma
equidecompasable한 두 $P=P_1 \cup \cdots \cup P_n$과 $Q=Q_1 \cup \cdots \cup Q_n$에 대해, 각 segment에 적절히 양의 개수만큼 pearl을 놓아 각 $P_k$의 edge와 그에 대응되는 $Q_k$의 edge 위에 놓여 있는 pearl의 개수가 같도록 할 수 있다.
증명은 위의 Cone lemma를 사용합니다. $P$의 분할에서 각 segment 위의 pearl의 개수를 $x_i$, $Q$의 분할에서 각 segment 위의 pearl의 개수를 $y_j$로 둡시다. 이때 $P$의 분할에서 각 $P_k$ 위 edge에 대해, 그와 대응되는 $Q_k$ 위 edge와 서로 pearl의 개수가 같도록 하는 양의 정수 $x_i$들과 $y_j$들을 찾아주면 됩니다.
그러면 $P_k$ 위의 edge $e$가 $s_i$들로 분할되고 $Q_k$ 위의 대응되는 edge $e’$가 $s_j’$로 분할된다 할 때, 위 조건을 수식을 이용하여 나타내면
\[\sum_{i : s_i \subseteq e} x_i - \sum_{j : s_j' \subseteq e'} y_j = 0\]와 같습니다.
그런데, 위는 $x_i$들과 $y_j$들로 이루어진 선형 연립 방정식이고, 각 $x_i$들과 $y_j$들을 해당 segment의 길이로 두게 되면 위 선형 연립 방정식은 양의 실수해를 가짐을 알 수 있습니다. 따라서 Cone lemma에 의해 위는 양의 정수해 또한 가져야하고, 증명이 완료됩니다.
Bricard’s condition
(Theorem) 두 3차원 다면체 $P, Q$가 equidecomposable하고, 이때 각각의 이면각을 $\alpha_1, \cdots, \alpha_r$과 $\beta_1, \cdots, \beta_s$라고 할 때,
\[m_1 \alpha_1 + \cdots + m_r \alpha_r = n_1 \beta_1 + \cdots + n_s \beta_s + k \pi\]를 만족하는 양의 정수들 $m_i$와 $n_j$, 그리고 정수 $k$가 존재한다. 더 나아가, equicomplementable한 $P$와 $Q$에 대해서도 성립한다.
Hilbert’s third problem을 논증하기 위해서는 equidecomposable까지만으로도 충분하나, 확장형까지 증명해보도록 하겠습니다.
먼저, $P$와 $Q$가 equidecomposable하고, 그 분할을 $P = P_1 \cup \cdots \cup P_n$와 $Q = Q_1 \cup \cdots \cup Q_n$라 합시다. (이때 $P_i$와 $Q_i$는 합동.) 이때 Pearl lemma에 따라, 각 분할에 대해 segment마다 pearl을 잘 할당할 수 있습니다.
이제 $\Sigma_1$을 $P$의 각 분할에 대해 각 조각들의 pearl들을 기준으로 dihedral angle을 모두 더한 것으로 정의합니다. 이때 한 edge에 여러 pearl이 있으면 중복하여 셉니다.
그러면, 기본적으로 pearl이 $P$의 edge 위에 있을 때는, $P$의 어떤 $\alpha_j$가 더해지게 되며, 만약 $P$의 면 위에 있을 때는 공간 내 반 바퀴를 더 세므로 $\pi$만큼, 그리고 $P$의 내부에 있을 때는 $2 \pi$ 혹은 $\pi$만큼을 더 셈을 알 수 있습니다. (앞의 경우는 공간 내 한 바퀴를 더 셀 때, 뒤의 경우는 pearl이 어떤 $P_i$의 면 위에 있어 공간 내 반 바퀴를 더 셀 때 생김.)
따라서 어떤 양의 정수들 $m_j$와와 음이 아닌 정수 $k_1$에 대해 \(\Sigma_1 = m_1 \alpha_1 + \cdots + m+r \alpha_r + k_1 \pi\) 를 만족하고,
마찬가지로 $Q$에 대해 $\Sigma_2$를 정의하게 되면 어떤 양의 정수들 $n_j$와 음이 아닌 정수 $k_2$에 대해 \(\Sigma_2 = n_1 \beta_1 + \cdots + n_s \alpha_s + k_2 \pi\) 임을 알 수 있습니다.
그런데, 이때 $\Sigma_1$와 $\Sigma_2$는 각 pearl들에 대해 $P_i$, $Q_i$들을 개별적으로 세어준 것으로 볼 수 있고, 이때 $P_i$와 $Q_i$가 합동이므로 $\Sigma_1 = \Sigma_2$임을 얻을 수 있고, 따라서 Bricard’s solution을 얻게 됩니다. ($k=k_2-k_1 \in \mathbb{Z}$)
이제 $P$와 $Q$가 equicomplete하다 합시다. 즉, 합동인 $P_i’‘$와 $Q_i’‘$에 대해 $\tilde{P} = P_1’’ \cup \cdots \cup P_n’‘$와 $\tilde{Q} = Q_1’’ \cup \cdots \cup Q_n’‘$을 만족하고, 합동인 $P_i’, Q_i’$들에 대해 $\tilde{P} = P \cup P_1’ \cup P_2’ \cup \cdots \cup P_m’$과 $\tilde{Q} = Q \cup Q_1’ \cup Q_2’ \cup \cdots \cup Q_m’$을 만족한다 합시다. 그리고 아까와 같이 Pearl lemma에 따라 위 4개의 분할에서 각 segment에 pearl을 놓는데, $\tilde{P}$의 두 분할에서 각 edge의 pearl의 개수의 합이 똑같도록 놓고, $\tilde{Q}$도 마찬가지로 놓습니다. (Cone lemma를 통해 Pearl lemma를 보이는 과정을 생각해보면, 이러한 restriction이 가능함을 알 수 있습니다.)
이제 방금과 같이 $\Sigma_1’$과 $\Sigma_2’$, 그리고 $\Sigma_1’‘$과 $\Sigma_2’‘$을 pearl들에 따라 더한 이면각의 합으로 정의합니다. 그러면, $\tilde{P}$와 $\tilde{Q}$가 equidecomposable하므로 $\Sigma_1’’ = \Sigma_2’‘$를 쉽게 얻을 수 있습니다. 또, $\Sigma_1’$과 $\Sigma_1’‘$은 동일한 다면체 $\tilde{P}$에 대해 각 edge 위에 같은 수의 pearl이 놓여 있으므로, 위 논리와 동일하게 어떤 정수 $l_1$에 대해 $\Sigma_1’ = \Sigma_1’’ + l_1 \pi$가 성립하고, 마찬가지로 어떤 정수 $l_2$에 대해 $\Sigma_2’ = \Sigma_2’’ + l_2 \pi$를 만족합니다.
따라서 정수 $l = l_2 - l_2$에 대해
\[\Sigma_2' = \Sigma_1' + l \pi\]가 성립함을 얻습니다. 그런데 $\Sigma_1’$과 $\Sigma_2’$는 각각 $\tilde{P}$와 $\tilde{Q}$의 분할이고, 각각 $P$, $Q$를 제외하면 서로 같은 조각들로 구성되어 있습니다. 따라서 양변의 $P_i’$ 항들과 $Q_i’$ 항들을 서로 소거시킬 수 있고, 이때 $P$와 $Q$의 항들만 남으므로 소거시킨 후의 각각의 항을
\[m_1 \alpha_1 + \cdots + m_r \alpha_r, \quad n_1 \beta_1 + \cdots + n_s \beta_s\]와 같이 표현할 수 있습니다. ($m_j$는 $P$의 이면각 $\alpha_j$를 이루는 edge 위의 pearl의 개수이고, $n_j$는 마찬가지로 $Q$의 이면각 $\beta_j$를 이루는 edge 위의 pearl의 개수.) 또, 위 둘의 차는 $l\pi$로 나타나므로
\[m_1 \alpha_1 + \cdots + m_r \alpha_r = n_1 \beta_1 + \cdots + n_s \beta_s + l \pi\]를 얻고, 증명이 완료됩니다.
Counterexample of Hilbert’s Thrid Problem
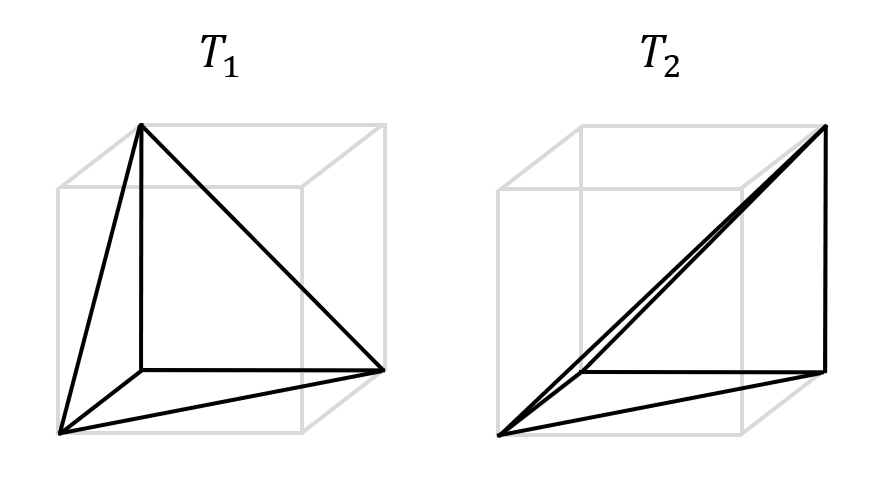
다음과 같은 두 다면체 $T_1$과 $T_2$를 생각해봅시다.
둘의 부피가 동일함은 쉽게 확인할 수 있습니다. 이때 각각의 이면각을 살펴봅시다.
$T_1$의 이면각들을 계산해보면, 세 개의 $\frac{\pi}{2}$와 세 개의 $\cos^{-1}\frac{1}{\sqrt{3}}$로 이루어짐을 쉽게 계산을 통해 알 수 있습니다.
또, $T_2$의 이면각을 계산해보면, 세 개의 $\frac{\pi}{2}$와 두 개의 $\frac{\pi}{4}$, 그리고 한 개의 $\frac{\pi}{3}$로 이루어짐을 알 수 있습니다. (마지막의 경우 정육면체를 공간대각선을 한 점으로 만들도록 사영시켜 정육각형으로 만들면 쉽게 관찰할 수 있습니다.)
따라서, 만약 $T_1$과 $T_2$가 equidecomposable하다면 Bricard’s condition에 의해 \(m \cdot \frac{\pi}{2} + n \cdot \cos^{-1}\frac{1}{\sqrt{3}} = r \cdot \pi + k \cdot \pi\) 인 정수 $m, n$과 유리수 $r$, 그리고 정수 $k$가 존재합니다.
그런데, 양변을 $\pi$로 나누고 정리하면 유리수 $p, q$에 대해
\[\frac{1}{\pi} \cos^{-1} \frac{1}{\sqrt{3}} = \frac{p}{q}\]임을 얻습니다.
하지만 $\frac{1}{\pi} \cos^{-1} \frac{1}{\sqrt{3}}$는 무리수이므로 모순이고, 따라서 $T_1$과 $T_2$는 equidecomposable하지 않음이 증명됩니다. 더 나아가, 둘이 equicomplement하지 않음도 알 수 있습니다.
Irrationality of $\frac{1}{\pi} \cos^{-1} \frac{1}{\sqrt{3}}$
위 증명에서 $\frac{1}{\pi} \cos^{-1} \frac{1}{\sqrt{3}}$가 무리수라는 사실이 쓰였는데, 이를 간단한 고등학교 수준의 내용만으로 증명할 수 있어 소개해봅니다.
위를 보이기 위해, 양의 홀수 $n \geq 3$에 대해,
\[\frac{1}{\pi} \cos^{-1} \frac{1}{\sqrt{n}}\]이 무리수임을 보여보겠습니다.
먼저 $\cos \alpha + \cos \beta = 2 \cos \frac{\alpha+\beta}{2} \cos \frac{\alpha-\beta}{2}$라는 사실로부터 시작합니다. 이 공식에 $\alpha = (k+1)\varphi$와 $\beta = (k-1)\varphi$를 대입하면
\[\cos(k+1)\varphi = 2 \cos\varphi \cos k \varphi - \cos (k-1) \varphi\]를 얻습니다.
이제 $\varphi$ 자리에 $\varphi_n = \cos^{-1} \frac{1}{\sqrt{n}}$을 대입하면, 어떤 $n$의 배수가 아닌 정수 $A_k$에 대해
\[\cos k \varphi_n = \frac{A_k}{\sqrt{n}^k}\]이 성립함을 귀납적으로 확인할 수 있습니다.
실제로 확인해보면,
\[\cos (k+1) \varphi_n = 2 \frac{1}{\sqrt{n}} \frac{A_k}{\sqrt{n}^k} - \frac{A_{k-1}}{\sqrt{n}^{k-1}} = \frac{2A_k - nA_{k-1}}{\sqrt{n}^{k+1}}\]이므로 $n$이 $3$ 이상의 홀수라는 가정으로부터터 귀납적으로 참임이 보여집니다.
이제 $\frac{1}{\pi} \varphi_n$가 유리수라고 가정해봅시다. 그러면, 어떤 정수 $k, l > 0$에 대해
\[\frac{1}{\pi} \varphi_n = \frac{k}{l}\]가 성립합니다.
그러면, $l \varphi_n = k \pi$와 위의 결과로부터
를 얻고, $\sqrt{n}^l = \pm A_l$이 정수이므로 $l \geq 2$이고 $n \mid \sqrt{n}^l$임을 얻습니다.
따라서 $n \mid A_l$이고, 이는 $A_l$이 $n$의 배수가 아니라는 가정에 모순이므로 주어진 수
는 무리수라는 결론을 얻게 됩니다.
따라서 이로부터
\[\frac{1}{\pi} \cos^{-1} \frac{1}{\sqrt{3}}\]이 무리수임을 알 수 있고, Hilbert’s third problem의 증명을 마무리하였습니다.
Ending
실제로 Dehn이 제시한 풀이는 다음과 같은 Dehn invariant를 이용하였습니다.
\[\sum_i l_i \otimes \theta_i\]이때 $l_i$와 $\theta_i$는 각각 다면체의 edge의 길이와 이면각을 나타냅니다.
하지만 이에 대해 다루는 것은 위의 풀이에 비해 상당히 복잡한 내용이고, 위의 풀이가 매우 간결하고 아름답다는 점에서 위와 같은 풀이를 소개하였습니다.
References
Martin Aigner & Günter M. Ziegler - Proofs from THE BOOK